0 前言

参考视频

1 图的存储

1.1 邻接矩阵

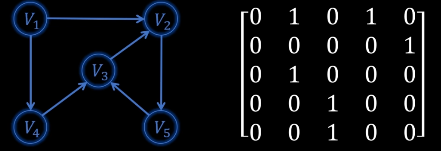
image-20260126163323373

代码实现

1
int matrix[n][m];

优点

  • 容易判断两个顶点间是否有边
  • 容易计算顶点的度

1.2 邻接表

1
2
3
4
5
// 定义一个vector数组
std::vector<int> adj[n];

//如果是带权图
std::vector<std::pair<int, int>> adj[n];

1.3 对比

degree是度的意思。

存储方案 空间复杂度 判断 i→j 是否有边 遍历所有邻居 适用场景
邻接矩阵 $O(n^2)$ $O(1)$ $O(n)$ 顶点数较少、稠密图
邻接表 $O(n + e)$ $O(degree(i))$ $O(degree(i))$ 顶点数较多、稀疏图

2 图的遍历

2.1 深度优先搜索（DFS）

深度优先搜索 (Depth First Search, DFS) 是一种用于遍历或搜索树或图的算法。它的核心思想是“不撞南墙不回头”：从起始节点开始，沿着一条路径尽可能深地探索下去，直到无法继续（到达叶子节点或已访问节点），然后回溯到上一个节点，继续尝试探索其他分支。

DFS 遵循“深度优先”策略。在访问一个起始顶点 $v$ 后，它会依次从 $v$ 未被访问的邻接点出发，进行深度优先遍历。

  • 数据结构：DFS 本质上是利用了栈 (Stack) 的后进先出 (LIFO) 特性。在代码实现中，通常使用递归（隐式使用系统栈）或显式定义的 std::stack
  • 状态标记：为了防止在图中陷入死循环（环路），必须维护一个 visited 数组来记录哪些节点已经被访问过

2.2 广度优先搜索（BFS）

广度优先搜索 (Breadth First Search, BFS) 是一种按“层”推进的遍历算法。它从起始节点开始，先访问所有距离为 1 的邻居，再访问所有距离为 2 的邻居，以此类推。

BFS 遵循“横向扩展”策略。它会先均匀地向四周探索，只有当这一层的所有节点都被访问过后，才会进入下一层。

  • 数据结构：BFS 核心是利用了队列 (Queue) 的先进先出 (FIFO) 特性
  • 状态标记：与 DFS 一样，必须使用 visited 数组记录已访问节点，防止死循环
  • 最短路径性质：在无权图中，BFS 第一次到达某个节点时，所经过的路径长度一定是该节点到起点的最短路径

3 回路

3.1 欧拉回路

从一个点出发，刚好经过每条边一次，然后回到原点，每个点要有进有出，即每个点的度必须是偶数。

eg：一笔画问题。

3.2 汉密尔顿回路

从一个点出发，沿着边走，刚好经过每个顶点一次，之后回到出发点。

4 拓扑排序

有向无环图里所有顶点的线性序列，其中：

  • 所有顶点出现且只出现一次
  • 若存在一条A->B的路径，序列中A一定在B前面

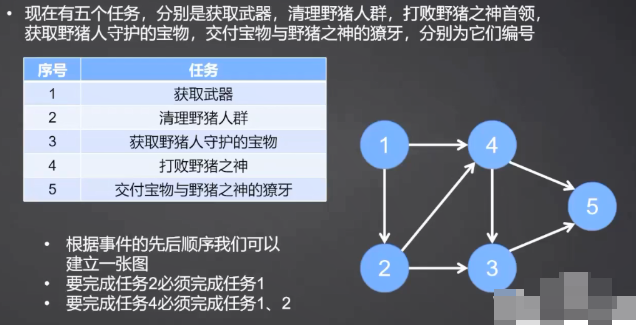
image-20260126210740604

如何找拓扑排序：

  • 从图里选择一个没有前驱（入度为0）的顶点
  • 从该图中删除该顶点和以它为起点的有向边

每个有向无环图有一个或多个拓扑排序。

5 最小生成树

最小生成树使图联通并且所有边的权值之和最小。

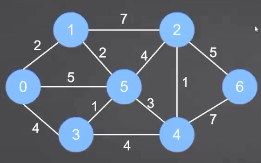
image-20230104220908055

5.1 Prim算法

普利姆算法。

  • 从任意节点出发来寻找最小生成树
  • 某个点加入到被选取的点中后，解锁这个点出发的所有新的边
  • 在所有解锁的边中选最小的边，然后看看这个边会不会形成环
  • 如果会，不要当前边，继续考察剩下解锁的边中最小的边，重复3）
  • 如果不会，要当前边，将该边的指向点加入到被选取的点中，重复2
  • 当所有点都被选取，最小生成树就得到了

5.2 Kruskal算法

克鲁斯卡尔算法。

  • 总是从权值最小的边开始考虑，依次考察权值依次变大的边
  • 当前的边要么进入最小生成树的集合，要么丢弃
  • 如果当前的边进入最小生成树的集合中不会形成环，就要当前边
  • 如果当前的边进入最小生成树的集合中会形成环，就不要当前边
  • 考察完所有边之后，最小生成树的集合也得到了

6 最短路径

某点到某点的最短路径。

6.1 Floyd算法

弗洛伊德算法。

特点：多源算法，一次性计算出所有点之间相互的最短距离，可以处理负权边。

Floyd算法的核心是动态规划，阐述为：i到j的最短距离要么等于i直接到j的距离，要么等于i间接到j的距离。

即：

1
2
3
4
5
6
7
8
9
10
for(int k=0;k<n;k++){
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            if(dis[i][k]+dis[k][j]<dis[i][j]){
                dis[i][j] = dis[i][k]+dis[k][j];
                path[i][j] = path[k][j];
            }
        }
    }
}

path[0,4] = 3。

path[0,3] = 0，结束，那么路径为0->3->4。

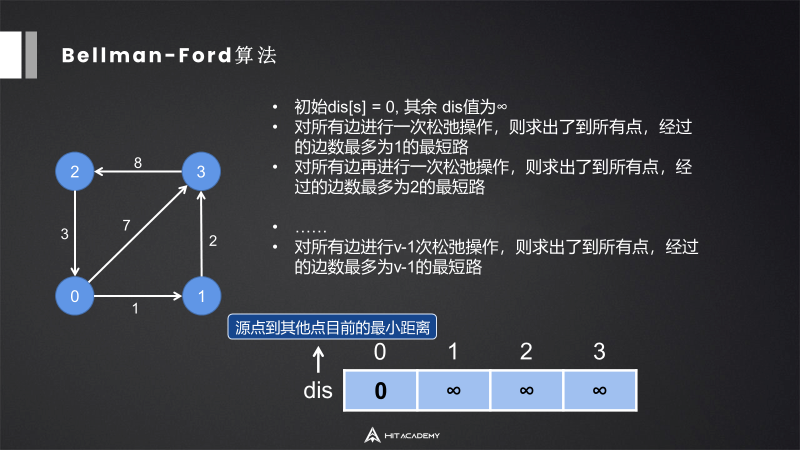
6.2 Bellman-Ford算法

特点：单源算法，动态规划，可以处理负权边。

松弛操作：只经过一条边可以到达哪些点。

image-20230105153750406

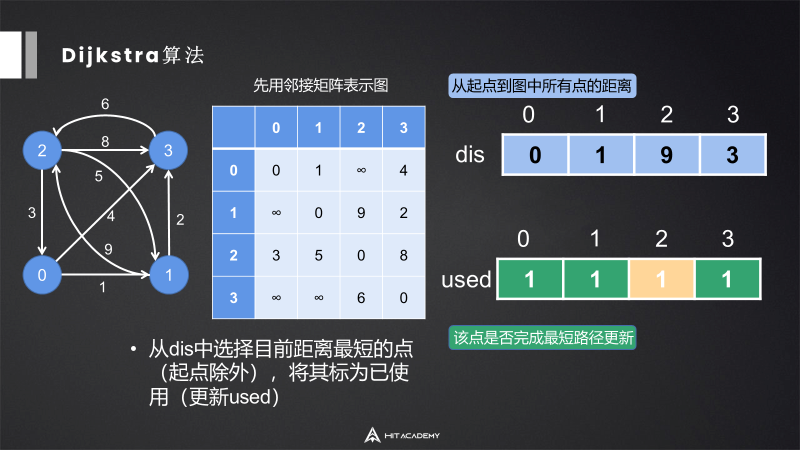
6.3 Dijkstra算法

迪杰斯特拉算法。

单源算法，不可以处理负权边，因为dijkstra的本质是贪心，如果出现负权边，那么已经完成过最短路径更新的点可能被推翻。

不断选择离已经相连的点最近的点。

image-20230105154753180

image-20230105154940211

6.4 区别

Floyd Bellman-Ford Dijkstra
时间复杂度 $O(V^3)$ $O(V*E)$ $O(V^2)$
空间复杂度 $O(V^2)$ $O(V)$ $O(V^2)$
源数 多源 单源 单源
负权处理能力 负权边 √ 负权回路 × 负权边 √ 负权回路 × 负权边 × 负权回路 ×

6.4 A*算法

视频

核心：代价公式$f(n) = g(n) + h(n)$

这是 A* 的灵魂，决定了算法下一步该往哪走：

  • $g(n)$：实际代价。从起点到当前节点 $n$ 的真实距离（已经走过的路）
  • $h(n)$：启发代价（Heuristic）。从当前节点 $n$ 到终点的估计距离（还没走但预测要走的路）
  • $f(n)$：综合代价。A* 每次都会挑选 $f(n)$ 最小的节点进行扩展

三种常见的启发函数（在不同的地图下，我们要选择不同的启发函数）：

  • 曼哈顿距离

    • 场景：只能上下左右走

    • 公式：$|x_1 - x_2| + |y_1 - y_2|$

  • 对角距离

    • 场景：八向走位
    • 假设 $dx = |x_2 - x_1|$，$dy = |y_2 - y_1|$
    • 公式：

  • 欧几里得距离

    • 场景：可以任意角度飞行（直线距离）

    • 公式：$\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$

6.5 JPS跳点搜索算法