更新中…

之前其实有大概把闫令琪老师的games101过一遍，但最近要开始学shader，又觉得有点忘完了，所以打算再重新学一遍，顺便做一点方便以后查阅的笔记。

2 线代基础

2.1 向量（Vectors）

2.1.1 定义

  • 向量的计算公式：$\overrightarrow{AB} = B-A$

  • 向量的两个属性

    • 方向

    • 长度

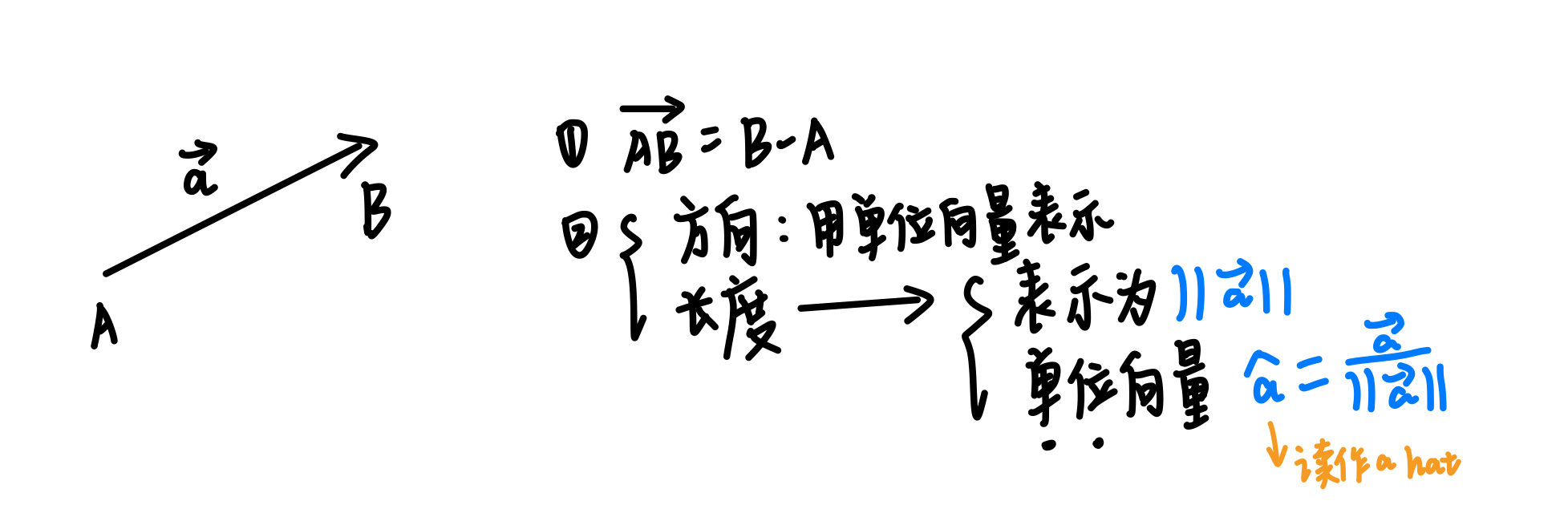
894687986ab9cc828ec4ae6cb201e6e

  • 向量在笛卡尔坐标系中的描述：$A = \binom{x}{y}$，$A^T = (x,y)$，$||A|| = \sqrt{x^2+y^2}$

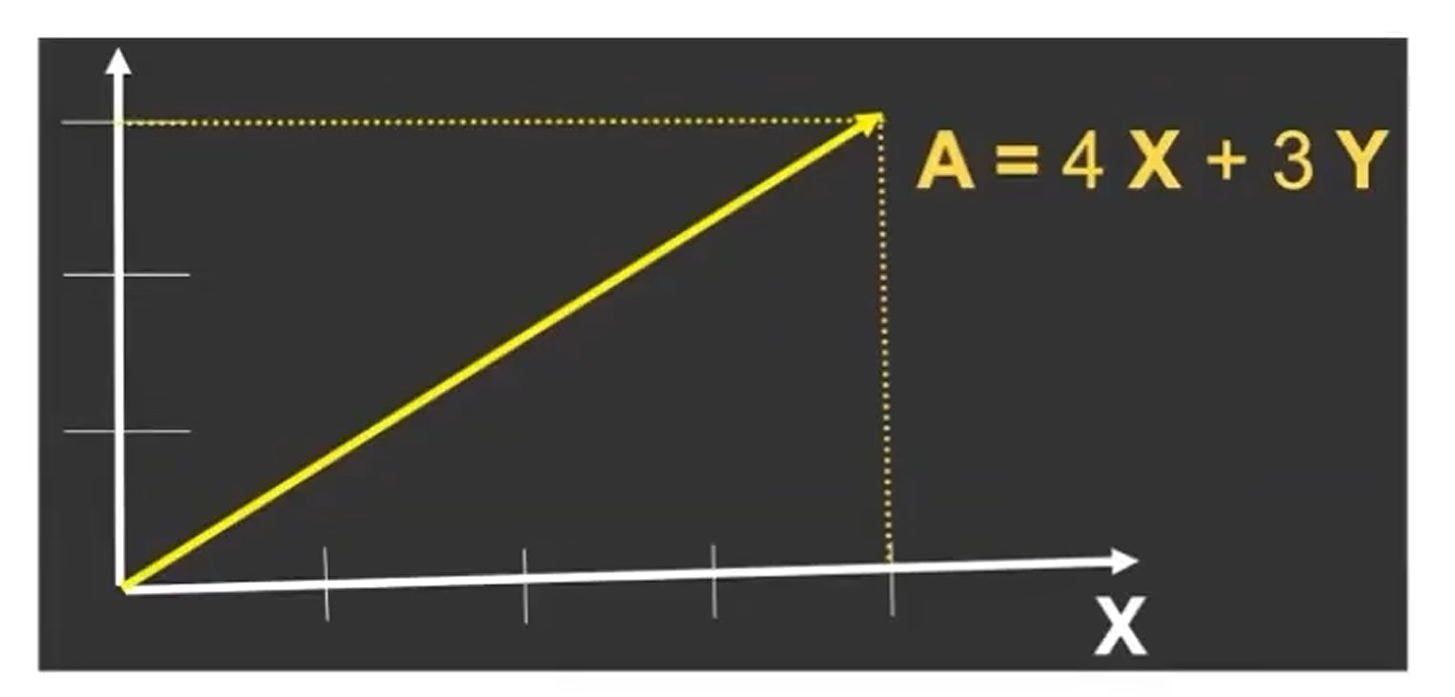
image-20240821223148182

2.1.2 向量的运算

1 Add-加

平行四边形法则 or 三角形法则

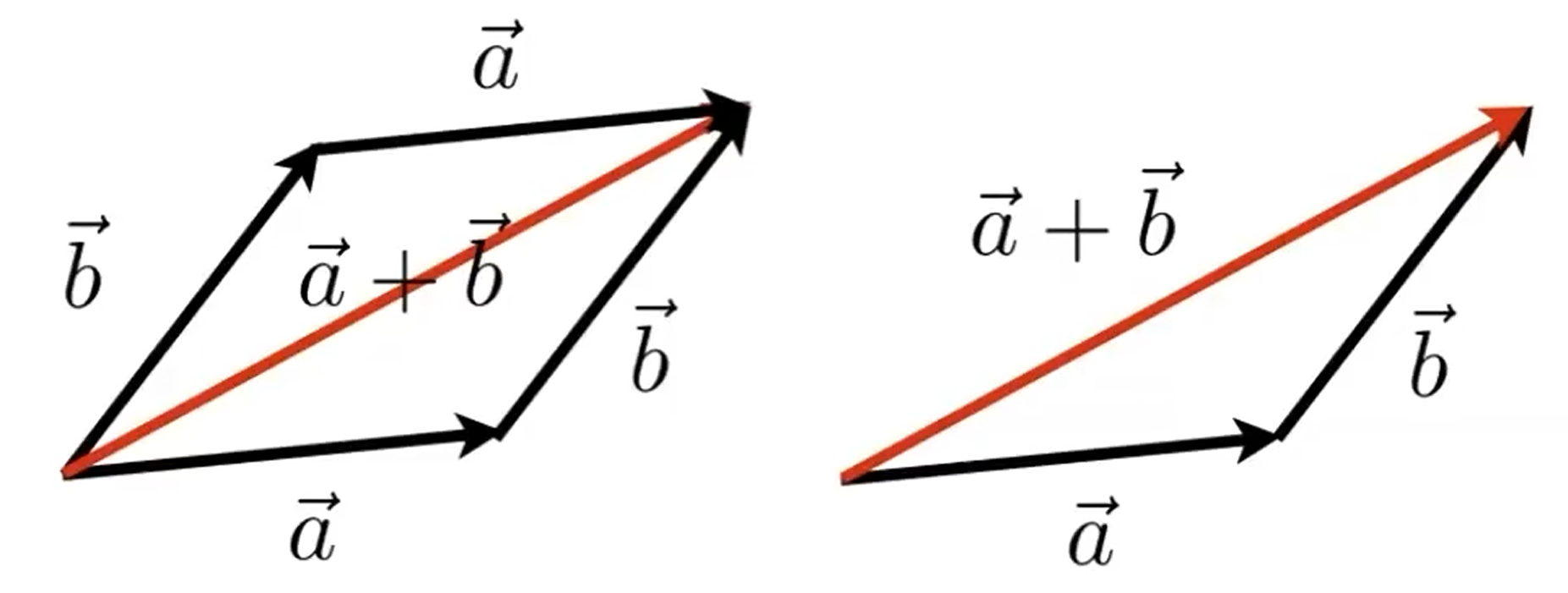
image-20240821222543685

2 Dot Product-点乘

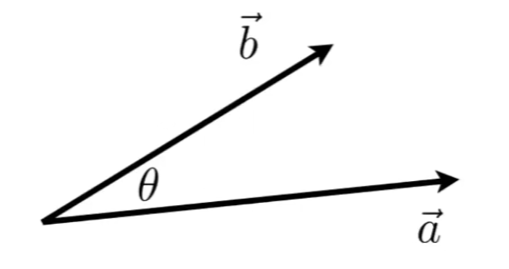
image-20240822193933513

点乘的计算

  • $\overrightarrow{a}· \overrightarrow{b}= ||\overrightarrow{a}||||\overrightarrow{b}||cosθ$

  • $cosθ = \frac{\overrightarrow{a}· \overrightarrow{b}}{||\overrightarrow{a}||||\overrightarrow{b}||}$

  • $cosθ = \hat{a}·\hat{b}$

  • 满足运算法则：交换律/结合律/分配律

点乘在笛卡尔坐标系中的运算

  • In 2D：$\overrightarrow{a}· \overrightarrow{b}=\binom{x_a}{y_a}·\binom{x_b}{y_b} = x_ax_b+y_ay_b$
  • In 3D：$ \overrightarrow{a}· \overrightarrow{b}= \begin{pmatrix} x_a \ y_a \ z_a \end{pmatrix}·\begin{pmatrix} x_b \ y_b \ z_b \end{pmatrix} = x_ax_b+y_ay_b+z_az_b$

点乘的几何意义

1.求一个向量在另一个向量上的投影。

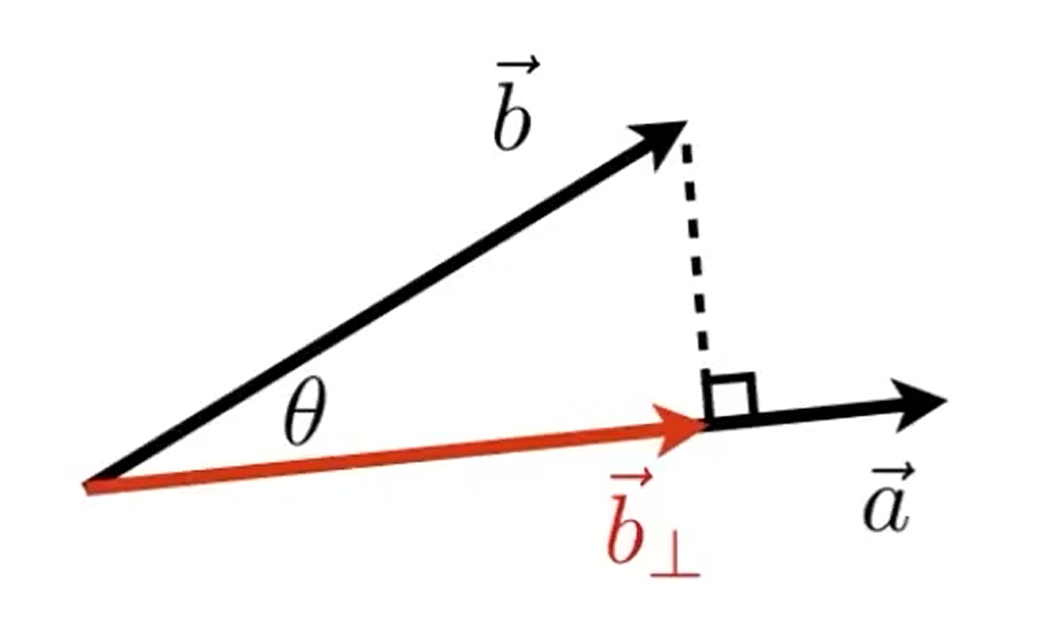
image-20240822200039731

$\text{Proj}{\vec{a}} \vec{b} = ||\text{Proj}{\vec{a}} \vec{b}||·\hat{a} = ||\vec{b}||cosθ·\hat{a}$

然后cosθ就可以用单位向量的点乘来算。

2.可以看出两个向量的“前后”关系。

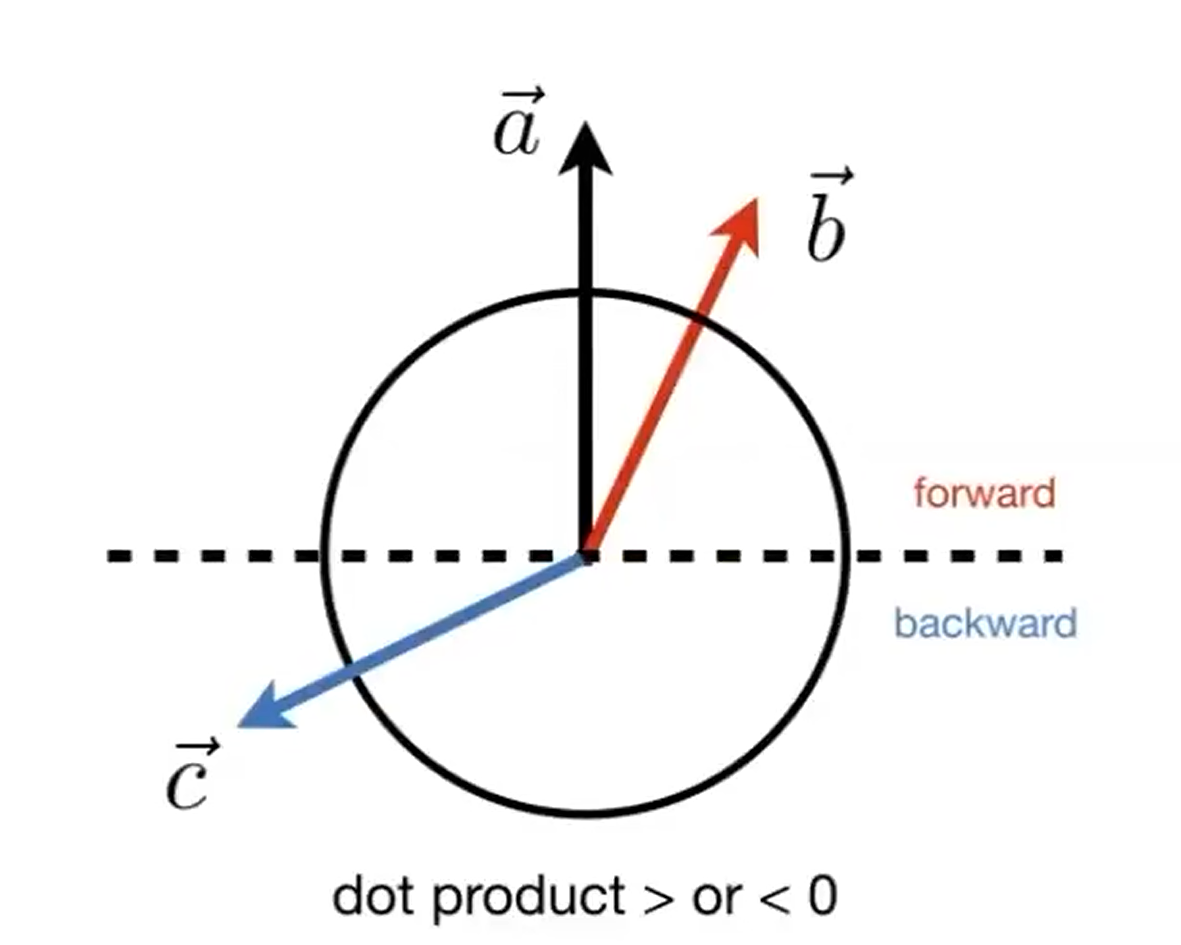
image-20240822201311731

3 Cross Product-叉乘

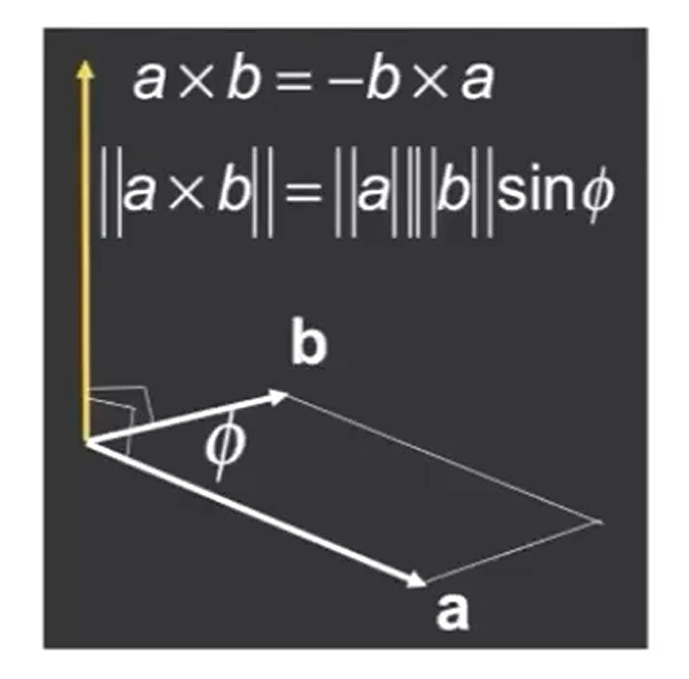
image-20240822201532747

两个向量的叉乘会得到一个新的向量，这个向量既垂直于$\vec{a}$，又垂直于$\vec{b}$，方向可以使用右手定则得到。

右手定则下：$\vec{x}×\vec{y} = +\vec{z}$

叉乘在笛卡尔坐标系中的运算

$\vec{a}×\vec{b} = \begin{pmatrix} y_az_b-y_bz_a \ z_ax_b-x_az_b \ x_ay_b-y_ax_b \end{pmatrix}$

叉乘的几何意义

①判断左和右 ②判断内与外